探索标准正态分布：Z值等于1.96意味着什么？

在统计学中，标准正态分布是一种非常重要的概率分布模型，它广泛应用于各种领域，包括社会科学、自然科学、工程学等。标准正态分布的一个关键特征是其平均数（均值）为0，标准差为1。在这种分布下，我们经常需要确定特定z值对应的概率，其中z值表示一个数据点距离平均数的标准偏差数。本文将探讨当z值等于1.96时的含义及其重要性。

1. 标准正态分布的基本概念

标准正态分布是一种连续概率分布，其概率密度函数由公式给出：⁄⁄[f(z) = ⁄⁄frac{1}{⁄⁄sqrt{2⁄⁄pi}}e^{-⁄⁄frac{z^2}{2}}⁄⁄]，其中⁄⁄(z⁄⁄)是任意实数。该分布的关键特性之一是它的对称性，以均值0为中心，左右对称。这意味着，对于任何给定的z值，都有一个相应的负z值，它们的概率相同。

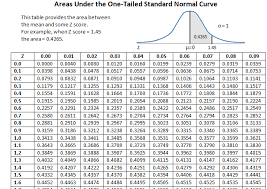
2. z值为1.96的含义

在标准正态分布中，z值为1.96具有特殊的意义。它代表了大约97.5%的数据位于平均值下方1.96个标准差之内。换句话说，只有2.5%的数据位于平均值上方超过1.96个标准差的位置。这一结论来自于标准正态分布表或z表，这些表格提供了不同z值下的累积概率分布。

3. 在假设检验中的应用

z值1.96在统计学中尤其重要，因为它常用于双尾假设检验中，特别是在显著性水平为0.05（即5%）的情况下。当进行此类测试时，如果计算得到的z值大于1.96或小于-1.96，那么可以拒绝原假设，认为所观察到的结果不是由于随机变异引起的，而是有统计学意义的证据支持备择假设。

4. 置信区间的构建

此外，在构建置信区间时，z值1.96同样扮演着关键角色。对于大多数实际应用而言，95%的置信水平是最常用的。在这个水平下，z值1.96用于计算置信区间的边界。具体来说，如果我们有一个样本平均数和已知总体标准差，可以通过以下公式来构建置信区间：⁄⁄[样本平均数 ⁄⁄pm (1.96 ⁄⁄times ⁄⁄frac{总体标准差}{⁄⁄sqrt{样本量}})⁄⁄]

综上所述，z值1.96在标准正态分布中具有重要意义，不仅在假设检验中作为判断是否拒绝原假设的临界值，也在构建置信区间时作为关键参数。理解并正确运用这一概念对于从事数据分析和研究工作的专业人士至关重要。通过掌握z值1.96的概念及其应用，我们可以更好地解释数据，做出更准确的预测，并基于数据驱动的决策提供有力的支持。