！奇函数相乘，结果竟然是……

在数学的浩瀚宇宙中，函数作为连接现实与抽象世界的桥梁，总是以其独特的魅力吸引着无数探索者的目光。今天，我们将踏上一场特别的旅程，去揭开一个关于函数性质的神秘面纱——奇函数乘奇函数等于什么？这不仅是一个数学问题，更是一次思维的碰撞与智慧的火花。

奇函数：数学中的“叛逆者”

首先，让我们来认识一下今天的主角之一——奇函数。在数学函数中，如果一个函数f(x)满足f(-x) = -f(x)的性质，那么我们就称它为奇函数。简单来说，奇函数就像是数学世界里的“叛逆者”，当输入值x变为-x时，它的输出值会“反方向”变化，就像是一个永远追求对立的精灵。

想象一下，如果你站在一个奇函数图像的正中心，向左走一步（即x变为-x），那么你在函数图像上的位置就会“跳”到对称的另一边，并且高度（即函数值）还会反转（变为原来的相反数）。这种对称性，正是奇函数最迷人的地方。

奇函数相乘：一场“叛逆”的盛宴

现在，让我们进入正题，探讨两个奇函数相乘的结果。想象一下，如果我们将两个这样的“叛逆者”放在一起，会发生什么呢？

假设我们有两个奇函数f(x)和g(x)，它们的乘积h(x) = f(x) * g(x)。为了理解h(x)的性质，我们可以尝试计算h(-x)：

h(-x) = f(-x) * g(-x)

= -f(x) * -g(x) （因为f和g都是奇函数）

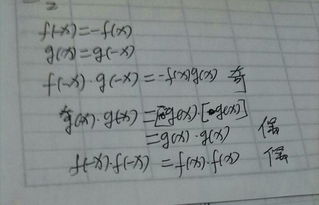
= f(x) * g(x)

= h(x)

奇迹出现了！我们发现，两个奇函数相乘的结果h(x)满足h(-x) = h(x)，这正是偶函数的定义。原来，当两个“叛逆者”携手合作时，它们共同创造出了一个“顺从”的结果——一个偶函数。这就像是在一场激烈的辩论中，两个持相反观点的人最终达成了一致，共同呈现出一个和谐的结果。

深入探索：背后的数学逻辑

这一发现背后隐藏着深刻的数学逻辑。奇函数和偶函数作为函数世界中的两大类基本性质，它们之间的相互作用和转换，不仅丰富了数学理论，也为我们解决实际问题提供了更多的工具和视角。

通过这次探索，我们不仅学会了奇函数相乘等于偶函数的结论，更重要的是，我们体验了数学探索的乐趣和魅力。数学不仅仅是一堆公式和定理的堆砌，它更是一种思维方式、一种探索未知世界的工具。

数学的无限可能

奇函数乘奇函数等于偶函数，这个简单的结论背后，蕴含着数学世界的无限可能和奥秘。每一次数学探索，都是一次思维的飞跃和智慧的启迪。希望这次旅程能够激发你对数学的兴趣和热爱，让你在未来的学习和生活中，勇敢地探索未知、追求真理。

在这场数学探索之旅的尾声，让我们再次回顾那个神奇的结论：奇函数乘奇函数等于偶函数。这不仅是一个数学公式，更是我们探索数学世界、追求知识之光的见证。让我们带着这份热情和好奇心，继续在数学的海洋中航行吧！